MATE AVANZADA 2014B : NOVIEMBRE

SEMANA 1

FUNCIONES ANALÍTICAS:

Definición:

f(z) es analítica en un Zo si y solo si f es derivable para todo z de algún disco D: |Z-Zo| < r .

También se enunciaron tres propiedades de las funciones analíticas:

i) Si la función f(z) = u(x,y) + iv(x,y) es analítica en algún dominio, entonces u y v satisfacen las ecuaciones de Cauchy-Riemann para todo (x,y) del dominio.

*Las Ecuaciones de Cauchy-Riemann (E.C.R.) son dos:

ii) Si u(x,y) y v(x,y) y sus primeras derivadas parciales son continuas, y cumplen las Ecuaciones de Cauchy-Riemann, entonces f(z) es analítica.

iii) Si f(z) es analítica en un cierto dominio, entonces u y v son Armónicas, es decir cumplen con dos expresiones de las ecuaciones de Laplace.

Ecuaciones de Laplace:

SEMANA 2

Demostrar que f(z) es analítica en z ≠ (0,0)

si z= x+iy

i) Las funciones u(x,y) y v(x,y) son continuas.

ii)

son continuas.

iii) Por demostrar que cumplen las E.C.R:

Como ambas condiciones cumplieron entonces f(z) satisface las E.C.R y por lo tanto f(z) es analítica en z ≠ (0,0).

Se realizó un ejercicio para determinar si las componentes u y v de f(z) son armónicas.

→ u y v son armónicas.

Se realizó un ejercicio donde se pide analizar si una función es analítica en un punto, para lo cuál se analizan las derivadas parciales con la definición de derivada cuando el límite tiende a un punto.

También se demostró que la función exponencial de z es analítica:

Finalmente se presentaron varias expresiones de funciones trascendentes:

En esta clase se inció con el tema de integrales de funciones de varibales complejas.

INTEGRACIÓN EN EL PLANO COMPLEJO

En principio se aplican las propiedades de integración de funciones reales excepto en las funciones que son eminentemente complejas (modulo y conjugada de z).
Para integrales indefinidas de funciones analíticas se mantiene la relación de las funciones reales pero hay ciertas diferencias, tales como:

En el caso de números reales la integral se mantiene como una aproximación de la suma de Riemann.

Las integrales en el plano complejo se analiza en una curva "c" en lugar de las sumas de Riemann.

Para las funciones de variable compleja las integrales cerradas presentan propiedades especiales (Integrales de Cauchy).

Integrales Indefinidas: Si esque f(z) tiene antiderivada se puede evaluar esta integral.

Ejemplos:

Curvas en el plano complejo:

Se denomina gama al conjunto de puntos (x,y) en el palo complejo.

La Ecuación de la curva gama parametrizada (función de t) es esta:

Los puntos evaluados en z de a y b son los punto extremos de la curva.
Si los puntos de evaluados en z de a y b son los mismos, se trata de una curva cerrada.
El sentido positivo de la curva se reconoce por el aumento de t.

Ejemplos:

Ecuación cartesiana de la circunferencia de centro en el origen y radio R.

Pasando a la forma parametrizada:

Entonces z(t) es expresado así:

Para un segmento de recta cualquiera se expresa de la siguiente manera:

Observaciones:

Dado que x(t) y y(t) son continuas en [a,b] y suponemos que existen x'(t) y y'(t) entonces se dice:

Si z'(t)≠0 entonces la curva es suave o derivable en ese [a,b].

Cuando una curva no tiene putnos dobles se le cononoce como Curva Simple o Curva de Jordan.
Una Curva Suave por intervalos es aquella que está formada por curvas suaves.

SEMANA 3

En esta clase se trabajó con la definición de una curva suave o diferenciable (o que no presenta picos) sabiendo que se debe cumplir que z'(t)≠0 para todo t elemento de su dominio.

INTEGRALES DE LÍNEA:

Para estas integrales se reocnocieron 5 propiedades importantes:

Si gama es una curva suave a intervalos y f(z) es una función continua entonces existe una integral de línea sobre la curva gama.

La suma o diferencia de dos integrales de diferentes funciones sobre la misma curva se puede expresar como la interal de la suma o diferencia de las funciones sobre esa curva.

La constante que multiplique a la función de integración puede ser extraida de la integral.

La integral de una función sobre una curva es igual al negativo de la integral sobre el negativo de la curva.

Si gama es una curva suave representada por z=z(t), para un t entre a y b, y f(z) es continua en C, entonces:

Consideraciones:

Un conjunto simplemente conexo (D) es aquel que solo contiene puntos de D, es decir no tiene huecos en su dominio.

Propiedad 6:

Si gama es una curva suave a intervalos de un z inicial a un z finalen un dominio simplemente conexo, f(z) es analítica en D y tenga antiderivada en el dominio D, entonces:

CONJUNTO SIMPLEMENTE CONEXO

Sea una curva suave o suave por intervalos de z1 a z2 en su dominio simplemente conexo. Si f(z) es función analítica se cumple:

Integral Cerrada

La curva es cerrada en la integral de línea.

Propiedad 1

Sea f(z) una función analítica en D, un dominio conexo y sea C una curva cerrada simple en D:

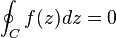$\oint_C f(z)dz = 0$ Integral de Cauchy

Propiedad 2

Si f(z) es analítica en un dominio simplemente conexo D, entonces la integral de línea es independiente de la trayectoria en D.

SEMANA 4

Propiedad 3 Teorema de la deformación

Sea f(z) analítica en D, excepto en zo y sean C y S curvas cerradas simples que encierran a zo, entonces:

Propiedad 4 Integral de Cauchy

Si f(z) es analítica en un dominio simplemente conexo D y sea C una curva cerrada simple que encierra a zo, entonces:

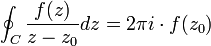
$\oint_C\frac{f(z)}{z-z_0}dz=2\pi i\cdot f(z_0)$

Propiedad 5 Fórmula de Cauchy para las derivadas de orden superior

Sea f(z) analítica en un dominio simplemente conexo, y sea zo un punto en D, entonces f(z) tiene derivadas de todos los ordenes en zo, y la "n"-esima derivada de f(z) en zo es: