SEMANA 1
En nuestra primera clase de Matemática Avanzada recibimos indicaciones generales por parte de nuestra profesora. Como la creación y objetivo de este blog, la digitalización de nuestros deberes y como llevaremos la materia durante este semestre.
LOS NÚMEROS COMPLEJOS
Recordamos la clasificación de los números:
Forma algebraica:
z=a+ib
donde a e b pertenecen al campo de los reales; i es igual a la raíz de -1.
Parte real R(z)=a
Parte Imaginaria Im(z)=b
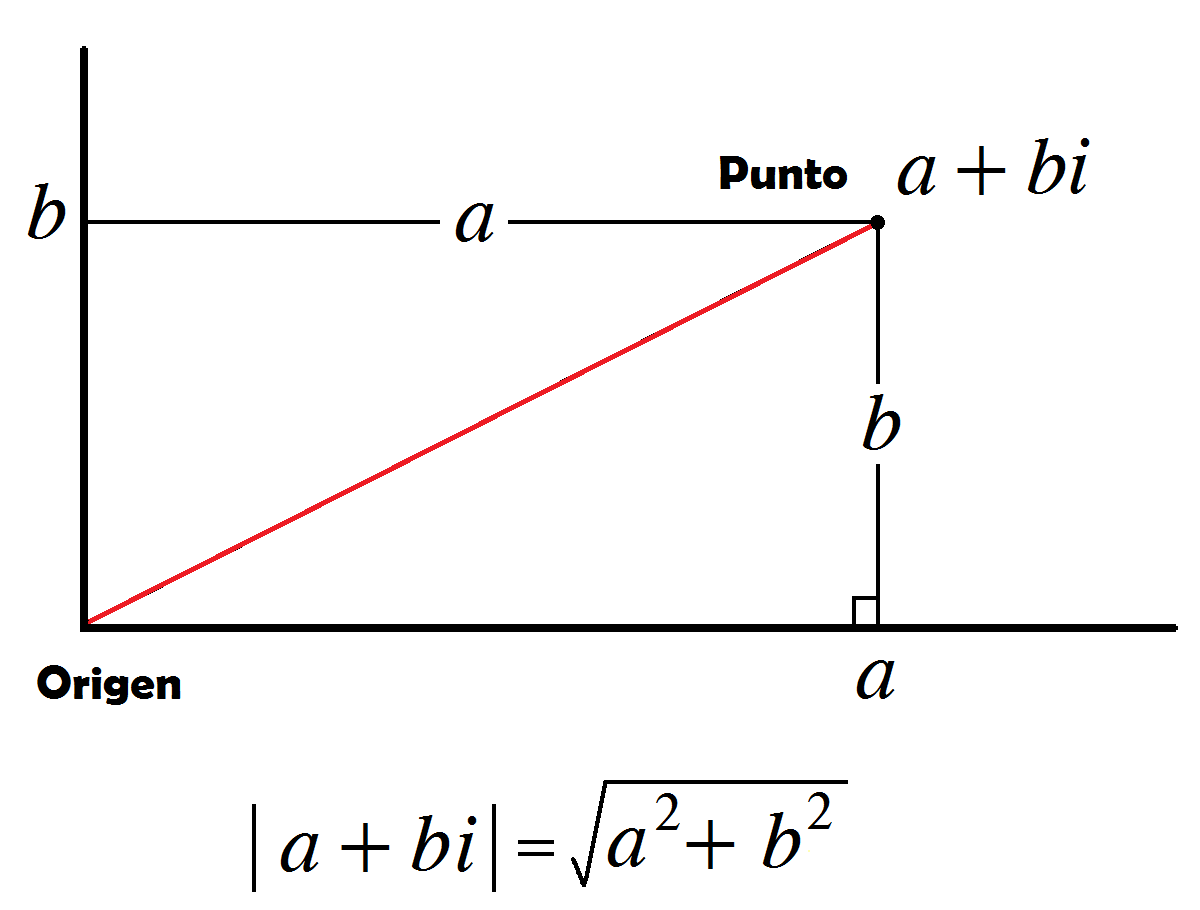
La imagen mostrada representa el plano complejo, constituido por un eje real Re(z) y un eje imaginario Img(z).
NOTA:
- Si Re(z) = 0 entonces z es un número imaginario puro. z=ib
- Si img(z)=0, entonces z es un número real. z=a
Potencias de i
Para poder determinar que valor le corresponde a un i elevado a la n, entonces se divide n para 4, y se toma en cuenta el residuo. Si el residuo es 0, entonces i^nerá equivalente a i^0. Si el residuo es 1, entonces i^n será equivalente a i^1. Así, es necesario solo es necesario deducir desde i^0 hasta i^4.
Conjugado de z
Dado z=x+iy, entonces su conjugado será:
(Conjugado de z) = x-iy
z*(Conjugado de z) = (x+iy)(x-iy)
=x^2 + y ^2
*Multiplicando por el conjugado desaparece la parte imaginaria*
División de complejos
Dado z1=a+ib y z2=c+id, entonces z1 / z2 =
SEMANA 2
Módulo de un complejo:
Donde:
|z|=(x^2+y^2)^(1/2)
z*(conjugado de z)= (x+iy)(x-iy)
= |z|^2
FORMA TRIGONOMÉTRICA
Del gráfico se tiene:
sen (theta) = y/r cos (theta) = x/r
y = r sen (theta) x = r cos(theta)
Donde theta es el argumento de z y r es el módulo de z.
Entonces para la transformación de rectangulares a polares:
z = x+iy
z = r cos (theta) + i r sen (theta)
z = r(cos (theta) + i sin (theta)) <-- Forma trigonométrica completa
z = r cis (theta) <-- Forma trigonométrica reducida *cis(theta) = cos (theta) + i sen (theta)
Para encontrar el argumento de z, dividimos y/x, obteniendo:
(theta) = arc tan (y/x)
Propiedades
Sean z,w números complejos, entonces se cumple:
1. z*(conjugado de z) = |z|
2. |z| |w| = |zw|
3. Si w es diferente de 0, entonces |z/w| = |z| / |w|
4. arg (zw( = arg (z) + arg (w)
5. arg (z/w) = arg (z) - arg (w)
6. Si a pertenece a los reales positivos, entonces z y z*a tienen igual argumento.
Producto
Dado z1 = r1 cis (theta1) y z2 = r2 cis (theta2), entonces:
z1*z2 = (r1cis (theta1)) (r2 cis (theta2))
z1*z2= (r1*r2)(cis (theta1 -theta 2))
División
Dado z1 = r1 cis (theta1) y z2 = r2 cis (theta2), y z2 diferente de 0, entonces:
z1/z2 = r1/r2 cis (theta1-theta2)
Potenciación
Radicación
Sea z = r cis (theta)
z^(1/n) = (r cis /theta))^(1/n) ; n es natural
z^n = r^(1/n) cis ((theta+2 π k)/n) ; k = 0,1,2, ... n-1
Exponenciales Complejos
La serie de maclurin para la función exponencial es:
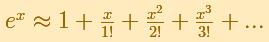
Y para los complejos es:
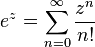
Fórmula de Euler:
Para demostrar esta fórmula se toma un imaginario puro (z=iy) , y se aplica la formula exponencial de la serie de Maclaurin e^z, obtenieéndose una parte real y una imaginaria. Qué observandolas bien la primera es la serie de Macalurin para el coseno y la segundo es la serie de Maclaurin para el seno.
A partir de está fórmula se pueden deducir las siguientes:

Ahora, si la forma polar la relacionamos con la forma exponencial, se podrá obtener:
z = r e^(iθ)obteniéndose así la forma exponencial de un número complejo.
SEMANA 3
Logaritmos de número complejos
FUNCIONES DE VARIABLE COMPLEJA
f : C---> C
z ---> w=f(z)
El conjunto de salida y el conjunto de llegada son los números complejos
Para calcular la imagen de z se la realiza como en las funciones reales.
Funciones de este tipo es complicado graficar en el plano ya que se parte de un par ordenado (x,y) y se llega a otro (a,b).
Algo más sobre las funciones de variable compleja:
Límites:
Al igual que en las funciones reales. De una función de variable compleja se puede obtener el límite. La definición de límite es similar a la estudiada en funciones reales.
En el siguiente enlace se muestra detalladamente la definición de límites y algunas propiedades:
SEMANA 4
Continuidad:
Cuando la función es discontinua existen dos posiblidades: Una que sea redefinible ( discontinuidad evitable) y la otra que no. Cuando el límite de f(z) cuando z-->z0, no existe entonces la discontinuidad es inevitable.
Derivadas:
ECUACIONES DE CAUCHY-RIEMANN
Las ecuaciones de Cauchy-Riemann son dos ecuaciones diferenciales parciales que son básicas en el análisis de funciones complejas de variable compleja, debido a que su verificación constituye una condición necesaria para la derivabilidad de este tipo de funciones.
Sea la funcion: f (z) = u(x,y) + iv(x,y)
Si la función f(z) es derivable en un punto zo= xo + iyo entonces deben verificarse las condiciones de Cauchy-Riemann:










No hay comentarios.:
Publicar un comentario